
Puzzles Numériques Pour Votre Cerveau

Puzzles Numériques Pour Votre Cerveau
Dans ce guide, nous offrons une gamme de conseils pratiques sur la façon de résoudre les puzzles de Kakuro, avec des difficultés allant du niveau débutant au niveau expert.
Pour résumer les règles : Kakuro est un jeu de puzzle sur un plateau en forme de mots croisés où les chiffres sont utilisés pour les faire correspondre aux valeurs spécifiées dans les carrés de définition du plateau. De plus, à l'intérieur de chaque groupe de somme, chaque chiffre peut apparaître une fois au plus.
La façon traditionnelle de résoudre un puzzle Kakuro est incrémentielle: en utilisant les informations existantes sur le tableau, vous pouvez trouver avec certitude la valeur d'une cellule spécifique qui ne peut prendre qu'une seule valeur possible. Ensuite, cette valeur est remplie et le processus est répété jusqu'à ce que toutes les cellules du tableau aient été découvertes.
Dans certaines situations, il n'y a pas de cellule de carte spécifique ayant une seule possibilité. Dans ces cas, chacune des possibilités doit être explorée seule et éliminée par des contradictions jusqu'à ce qu'il ne reste qu'une seule ligne de conduite.
Présentaient ci-dessous plusieurs méthodes pour faire des progrès dans la résolution du puzzle réel.
Il y a quelques définitions qui ne peuvent être résolus que d'une manière spécifique :
et ainsi de suite... Habituellement, vous pouvez survoler le numéro de définition sur une grille de Kakuro et une info-bulle apparaîtra contenant toutes les possibilités d'écrire cette somme avec des chiffres uniques dans le nombre de cellules disponibles.
Les sommes qui peuvent être écrites d'une manière unique sont généralement des montants faibles ou des sommes élevées qui obligent les chiffres faible/élevés dans la réponse pour les atteindre.
Avoir une façon unique d'écrire la somme aide, mais gardez à l'esprit que toutes les permutations sont valides et vous devez toujours déterminer quelle permutation réelle utiliser sur le tableau.
 |
 |
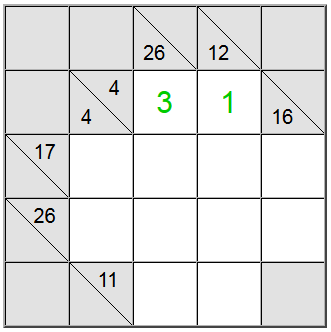 |
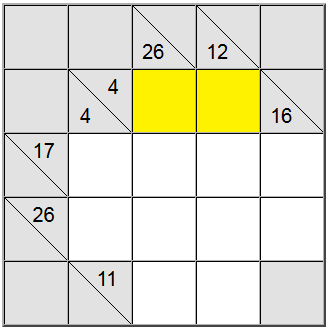
Pour les cellules jaunes surlignées ci-dessus, il n'y a qu'une seule façon d'écrire la somme : 4 = 1 + 3. Cependant, nous devons encore déterminer quelle permutation (1 + 3 ou 3 + 1) utiliser.
Il s'avère que la définition verticale 26 nous aide : une somme sur 4 cellules qui contiendrait le chiffre 1 serait au plus 1 + 9 + 8 + 7 = 25. Puisque notre somme est de 26, il s'avère que le chiffre 1 ne peut pas faire partie de la somme. Par conséquent, le seul ordre restant pour les carrés jaunes est 3 + 1.
 |
 |
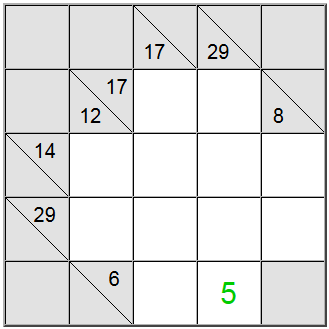 |
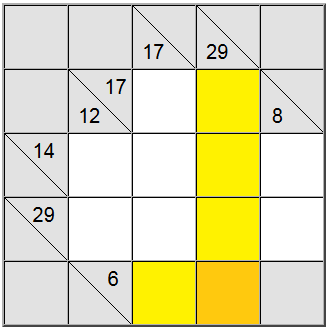
Sur le tableau ci-dessus, les carrés jaunes horizontaux peuvent être écrits comme 6 = 1 + 5 ou 6 = 2 + 4. La somme jaune verticale ne peut être écrite que comme 29 = 5 + 7 + 8 + 9.
Le carré jaune qui se trouve à l'intersection de ces deux définitions de somme doit contenir le même chiffre, de sorte qu'il doit y avoir un chiffre commun présent dans les définitions horizontales et verticales afin d'être partagé entre elles. En examinant les possibilités ci-dessus, nous pouvons facilement comprendre que 5 est le seul chiffre qui respecte ce critère.
Cette technique fonctionne particulièrement bien lors de l'intersection d'une somme basse avec une définition de somme élevée. Les définitions à somme basse et à somme élevée sont celles qui ont un nombre relatif de définition de somme faible ou élevée (6 et 29 respectivement pour notre exemple) par rapport au nombre de cellules disponibles. Comme 6 est relativement faible, il forcera des chiffres faibles dans la représentation de la somme, et 29 forceront des chiffres élevés (afin d'atteindre ces sommes en utilisant le nombre donné de cellules). Par conséquent, l'intersection des chiffres bas et élevés ne contient probablement qu'un seul candidat pour la valeur réelle de la cellule.
 |
 |
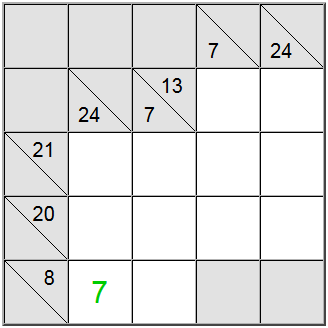 |
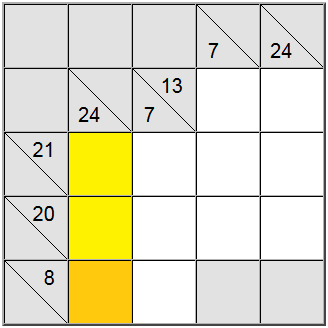
Parfois, il est utile de déterminer la valeur maximale ou minimale pour un groupe de somme. Cela peut vous donner une idée de la plage valide de chiffres pour cette somme particulière, ce qui à son tour vous aidera à établir une corrélation avec d'autres restrictions et à déterminer les affectations uniques sur le tableau.
Dans l'exemple ci-dessus, les cellules verticales jaunes acceptent uniquement des valeurs égales à 7 ou plus. Si vous essayez d'attribuer un 6, vous pouvez facilement comprendre que 6 + 9 + 8 = 23 de sorte que la somme de définition de 24 ne serait pas réalisable.
Comme 7 est un minimum, la définition horizontale ayant 8 comme somme force le 7 dans cette position.
Pratiquer est la meilleure façon de voir comment ce conseil peut être appliqué dans les jeux Kakuro réels. Jouez un puzzle pour de vrai. Nous vous souhaitons bonne chance et beaucoup de plaisir !
© 2026 - Tous droits réservés - Page Contact - Politique de confidentialité - CS | DA | DE | EN | ES | ET | FI | FR | HR | HU | ID | IT | JA | LT | LV | NL | PL | PT | RO | SV | TR